EL PROBLEMA DEL CASTOR LABORIOSO
En esta entrada, voy a hablar del problema del castor laborioso, un problema que fue propuesto por un matemático húngaro en 1962, llamado Tibor Radó, como uno de los primeros problemas de función no computable.
¿Cuál es el problema?
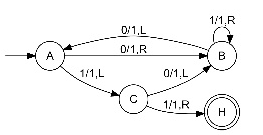
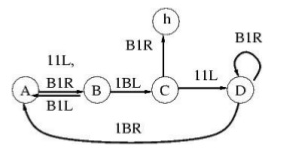
El problema consiste principalmente en la utilización de una Máquina de Turing (MT) de un cierto número de estados finito para generar el mayor número de unos posible para ese número de estados y se pare. (El número de unos que se puede generar varía en función al número de estados que se utilicen para la generación de la MT)
Lo curioso para este problema es que un número de estados de la MT mayor o igual a 5 no se sabe con total seguridad cuál es el número máximo de unos que se pueden generar sobre la cinta.
¿Qué se debe cumplir?
La Máquina de Turing tiene que cumplir dos condiciones esenciales:
- El alfabeto de la cinta solo puede tener dos valores: {Blanco, 1}
- La cinta inicialmente está en Blanco en todas sus posiciones.
Soluciones para N<=5
Como bien he dicho, para el numero de estados mayor o igual que 5 no se puede saber con total seguridad el número máximo de unos que se pueden generar, pero para n<5, sí que se sabe vamos a ver cada uno de estos autómatas por separado:
- Problema del Castor Laborioso resuelto con 1 Estado:
- Problema del Castor Laborioso resuelto con 2 Estados:
- Problema del Castor Laborioso resuelto con 3 Estados:
- Problema del Castor Laborioso resuelto con 4 Estados:
Evolución a lo largo de la historia
Poco a poco, la generación de unos para los diferentes estados ha ido aumentando. En esta tabla se ven los últimos datos de los récords en cada estado, como bien se puede comprobar lo dicho anteriormente, el número de unos es mayor cuando el numero de estados aumenta.
Número de estados
|
Nº de unos
|
Movimientos del cabezal
|
Autor/es
|
1
|
1
|
1
|
Lin y Rado (1962)
|
2
|
4
|
6
|
Lin y Rado (1962)
|
3
|
6
|
21
|
Lin y Rado (1965)
|
4
|
13
|
107
|
Brady (1975)
|
5
|
4098
|
47.186.870
|
Marxen y Buntrock (1990)
|
6
|
1.29149x10^865
|
3.00233x10^1730
|
Marxen (2002)
|
La mayor cantidad de unos generados por esos estados son los que indica la tabla, pero eso no quiere decir que sea el máximo que se pueden conseguir (para n>=5), estos "récords" se pueden seguir mejorando a lo largo del tiempo. Aunque alguno de estos récord son de hace mas de 20 años por lo tanto se habla de que pueden ser el máximo aunque no haya podido demostrarse, tampoco ha podido superarse.
Conclusión
En resumen, el problema del castor laborioso, es un problema que fue de los primeros que se descubrieron que no eran computables, a lo largo de los años se ha ido mejorando, pero actualmente no se puede saber con total certeza si se ha llegado al máximo número de unos generados por cada numero de estados puesto que es algo que no se puede calcular con nuestros métodos matemáticos, por lo tanto es una incógnita entre muchas que seguramente se resuelva en un futuro próximo o lejano.
José Luis Muñoz Peinado
Biblografía:
- http://matemalescopio.over-blog.es/article-matematicos-del-dia-76370027.html
- http://www.slideshare.net/deusto/el-problema-de-parada-y-los-castores-laboriosos-alan-turing-year
No hay comentarios:
Publicar un comentario